Viaggio nella matematica: dalle origini a problemi ancora irrisolti

La matematica spesso appare come un prodotto concluso, a volte lontano dalla realtà. Ma questa disciplina non rappresenta niente di tutto ciò. Tra le varie diramazioni del sapere, essa è una tra quelle che maggiormente ha origine nella pragmatismo. Lontana dall’aver risolto ogni dubbio continua ad interrogarsi, scavando per trovare le sue risposte.

La concretezza della matematica

Indagando le origini di questa disciplina, si può apprezzare il suo senso pratico. Nasce, infatti, per la contabilità statale. Probabilmente l’uomo iniziò a contare con le dita ma, in un secondo tempo, sentì la necessità di tenere memoria di quanto numerato. I metodi utilizzati a questo fine sono vari e differenti.

Quipu

Uno dei più antichi è quello dei quipu (parola che nella lingua degli Incas significa “nodo”). Si tratta di uno strumento di conteggio costituito da funi e nodi. Questo dispositivo era molto importante all’interno dello stato, tanto che vi era una figura ‘’specializzata’’ addetta ad utilizzarlo. Si tratta del quipucamayoes (“guardiano dei nodi“), funzionario incaricato a registrare nascite, matrimoni, decessi e altri dati utili all’amministrazione locale.

Bolla

Altro metodo di conteggio si basava sull’utilizzo di pietre. Spesso venivano usate nella vendita di bestiame per verificare la correttezza dell’acquisto. Infatti, i greggi, venivano accompagnati da un involucro di argilla, detto bolla. Al suo interno vi erano le pietre che corrispondevano al numero di capi di bestiame da vendere. Da qui deriva il termine ‘’bolla di accompagnamento’’, ancora oggi comunemente utilizzato. Col tempo però, le bolle sono state sostitute da tavolette di argilla. Dall’evoluzione di tale metodo si giunge poi alla nascita del testo inciso, sottoprodotto, almeno in origine, della scrittura numerica.

Nascita della geometria

Anche la nascita della geometria è legata alla risoluzione di un problema concreto. Dobbiamo agli Egizi lo studio di questa branca della matematica.  Gran parte delle attività delle popolazioni che abitavano questa zona, in antichità ruotavano attorno al Nilo. Le piene periodiche però, distruggevano i campi coltivati nei suoi pressi, elidendo i confini.  Una volta finito il periodo di piena, era dunque necessario trovare un modo per calcolare l’appezzamento di terreno che spettava ad ogni persona per ristabilire i confini. A tale scopo nacque la geometria.

E lo zero?

Lo zero (dall’arabo sifr “nulla”), rappresenta una delle dieci basi su cui si fonda la nostra scala numerica. Proprio a causa delle sua importanza nel mondo contemporaneo, sembra strano pensare che nell’antichità non ne esistesse il concetto. In origine, non aveva senso scrivere una quantità nulla, in quanto il computo presupponeva l’esistenza di oggetti da numerare. Quindi, quando si avevano numeri che presentavano lo zero in una delle cifre di cui si componevano, si creavano problemi di trascrizione.

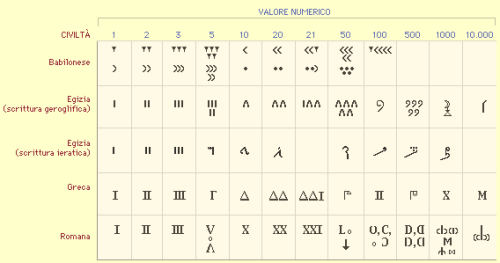
La prima comparsa dello zero risale all’epoca dei Sumeri, circa 3 mila anni fa. Era un simbolo cuneiforme e indicava l’assenza di un numero. Il suo sviluppo in senso moderno, va fatto risalire alla cultura Hindu, anche se il padre di tale numero è considerato il matematico arabo Muhammad ibn Musa al Khwarizmi. Il suo utilizzo rese i calcoli più rapidi e precisi. Il termine “zero” fu usato per la prima volta in Occidente dal matematico Leonardo Fibonacci nel 1202.

Le nostre sfide

La matematica di oggi, invece, su cosa si interroga? Quali sono i passi in avanti che abbiamo fatto? 

Nel maggio del 2000 Landon T. Clay ha messo in palio sette milioni di dollari per la risoluzione di altrettanti quesiti matematici, i cosiddetti “Problemi del Millennio“. Si tratta di interrogativi che ci poniamo da decenni. Vediamoli insieme:

1. L’ipotesi di Riemann: riguarda la distribuzione dei numeri primi. Riemann notò che questa è legata al comportamento di una funzione ben precisa: la “zeta di Riemann“. Dimostrare quest’ipotesi avrebbe anche ripercussioni nel mondo della crittografia, dove alcuni algoritmi si basano sulla difficoltà di trovare fattori primi di numeri spropositatamente grandi.
2. La teoria di Yang-Mills: utilizzata per spiegare le interazioni forti delle particelle elementari. Nonostante sia stata confermata dagli esperimenti, non è ancora stata compresa dal punto di vista teorico.
3. Il problema P versus NP: Gli P sono problemi matematici veloci da risolvere per i computer, mentre gli NP sono veloci da controllare, ma non necessariamente da risolvere. Ci si chiede, dunque, se un problema la cui risposta può essere verificata rapidamente può anche essere risolto velocemente. Molti considerano questo il più importante problema aperto nell’informatica.
4. Le equazioni di Navier-Stokes: spiegano il movimento dei fluidi nei loro moti turbolenti. La loro comprensione rimane per lo più oscura.
5. La congettura di Poincaré: uno dei più importanti problemi della topologia, risolto nel 2003 da Grigorij Jakovlevič Perel’man.
6. La congettura di Birch e Swinnerton-Dyer: riguarda le curve ellittiche nei numeri razionali. Se dimostrata, migliorerebbe anche la nostra conoscenza dei numeri primi.
7. La congettura di Hodge: è un problema di tipo topologico, di cui si deve dimostrare l’inverso.

Tra passato e avanguardia

La matematica mantiene ancora il suo fascino, nascondendo una storia fatta di quesiti. Ci ha accompagnato nell’evoluzione della nostra civiltà e continua a stimolare l’intelletto di chi gli si avvicina. Oggi le domande da porsi sono numerose. La bellezza sta nel continuare a studiare una disciplina che l’uomo stesso ha creato, e che, nonostante ciò, continua a scoprire. È un po’ come se conoscendo la matematica interrogassimo la nostra intelligenza.

Alessia Sturniolo

Bibliografia

• https://www.youtube.com;
• https://www.storicang.it;
• https://www.focus.it;
• https://www.superprof.it;
• https://www.thedifferentgroup.com;
• https://sciencecue.it;
• https://it.alegsaonline.com;