Aggiornamento Covid-19: proiezioni matematiche della pandemia

Sono passati diversi giorni dalla pubblicazione dell’articolo che spiegava la matematica del coronavirus. Tuttavia in quel periodo eravamo ancora agli albori, con una quantità di dati molto scarsa. Adesso i dati sono sufficienti per prevedere con buona accuratezza il futuro comportamento di questa terribile pandemia.

Bisogna però premettere che i modelli matematici applicati per studiare il virus non sono universali ed esatti, questo perché ad influenzare l’andamento del virus è anche il comportamento umano, e nessuna equazione matematica (almeno per ora) è in grado di prevedere le azioni degli esseri umani.

Tralasciando il comportamento umano, il virus si diffonde in una maniera piuttosto semplice: chi ne è portatore ha una certa probabilità di contagiare chi gli sta vicino. È ovvio quindi pensare che la crescita dell’epidemia è di tipo esponenziale, dato che nel corso di una giornata siamo a stretto contatto con 50 o anche più persone. Quindi, se fossimo infetti, avremmo trasmesso il virus ad una buona percentuale di loro, che diventeranno a loro volta portatori di virus.

Un esempio di andamento esponenziale è rappresentato in Figura 1, in cui si vede che il numero di infetti cresce senza sosta. Fortunatamente l’epidemia non si propaga in questo modo e la causa è dovuta a due fattori. Il primo è che il numero di umani, per quanto grande sia, è sempre un numero finito. Questo vuol dire che prima o poi l’epidemia si dovrà arrestare. Il secondo è che facciamo di tutto per non prendere il virus: ci isoliamo a casa, indossiamo le mascherine ed i guanti, tossiamo nel gomito, ecc…

Da queste considerazioni ci aspettiamo quindi che l’andamento dell’epidemia sia inizialmente esponenziale, ma che poi inizi a decrescere fino a fermarsi. In Figura 2 è rappresentato esattamente questo tipo di comportamento.

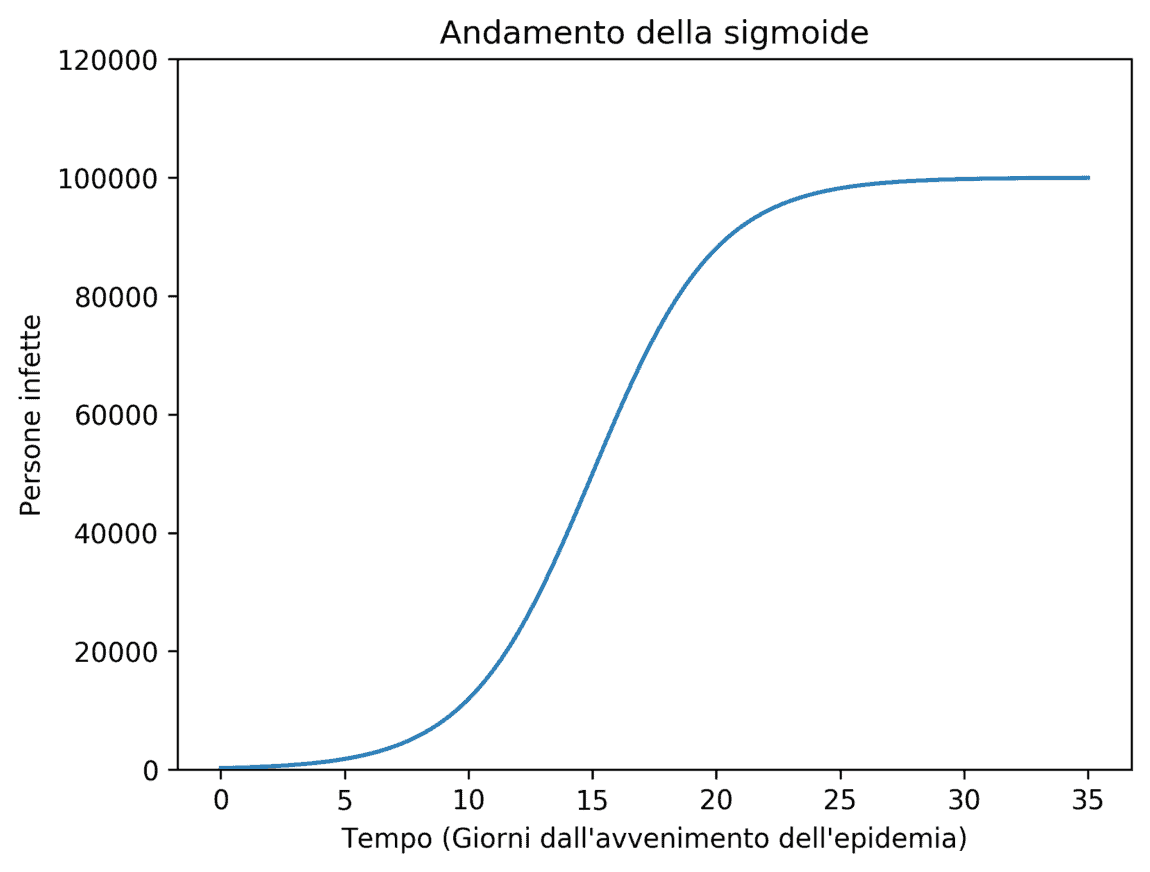
La funzione qui raffigurata si chiama sigmoide (o funzione logistica), ed è l’esempio più classico che si può considerare per un’epidemia.

Molti scienziati, durante questi mesi di quarantena, hanno cercato la teoria più appropriata per descrivere il coronavirus. La sigmoide è di sicuro un buon punto di partenza, ma presenta diversi difetti, come ad esempio il fatto di essere simmetrica. Per simmetria si intende che il modo in cui l’epidemia cresce è uguale al modo in cui decresce. Ma questo non è generalmente vero.

Le teorie più affermate sono:

• Gompertz
• Richards
• S.I.R.

Tutti questi modelli hanno una forma simile a quella di una sigmoide, ma presentano un’asimmetria. Per esempio la Figura 3, che rappresenta il caso della regione di Hubei in Cina, assomiglia molto ad una sigmoide, ma se si guarda con maggiore attenzione si può osservare che l’epidemia è scesa poco più velocemente della salita, manifestando così una lieve asimmetria. 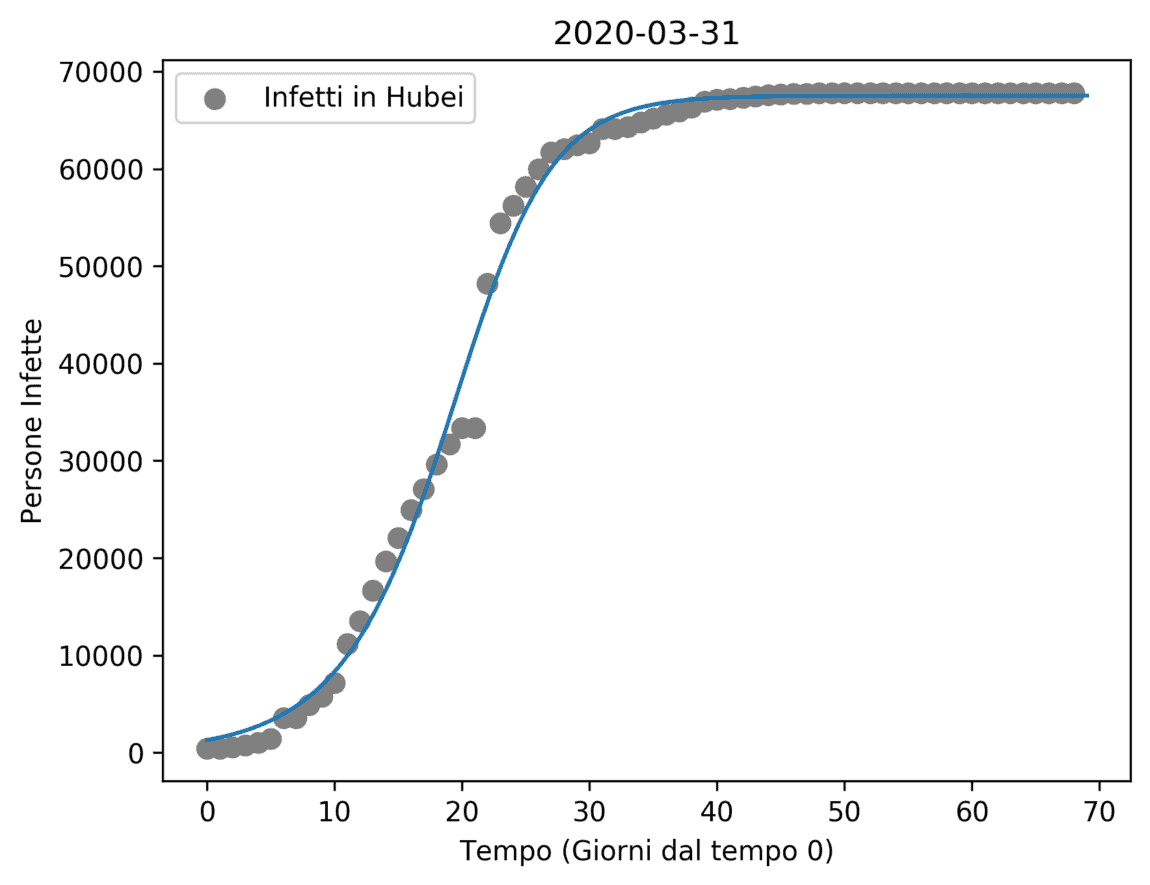La teoria a mio avviso più completa per lo specifico caso del COVID-19 è una versione modificata del modello S.I.R. [1]. Ma prima è opportuno spiegare il modello classico. (Per chi non ha voglia di addentrarsi nelle equazioni, può tranquillamente saltare questa parte).

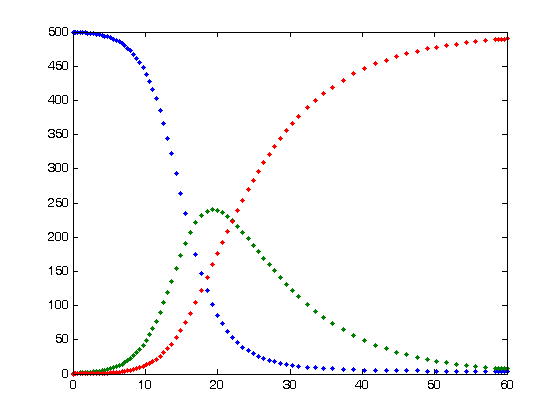
La sigla S.I.R. sta per Susceptible (Suscettibile), Infectous (Infetto), Recovered (Guarito). Questo modello infatti si occupa di descrivere l’andamento temporale di queste tre classi di persone.

Appartengono alla classe S le persone che non hanno ancora contratto il virus, e che quindi sono potenzialmente esposte al rischio. Alla classe I appartengono tutte le persone infette, e che quindi possono anche trasmettere il virus. Appartengono infine alla classe R tutte le persone che sono uscite dallo stato di infezione (che comprende sia i guariti che i deceduti).

Quali sono le equazioni matematiche che descrivono le quantità S,I ed R? Di certo non sono semplici, ma si possono fare alcune considerazioni. Col passare del tempo le persone suscettibili diminuiscono. Quanto diminuiscono? Dipende da quante persone a rischio ci sono e, ovviamente, dal numero di persone infette. Dire che le persone suscettibili diminuiscono significa che la sua variazione è un numero negativo.

Per quanto riguarda la variazione di persone ricoverate, questa è sicuramente una porzione delle attuali persone infette. Infine, la somma S+I+R deve dare il numero dell’intera popolazione (in questo caso dell’Italia). Queste considerazioni si traducono in “matematichese” in un sistema di equazioni differenziali:

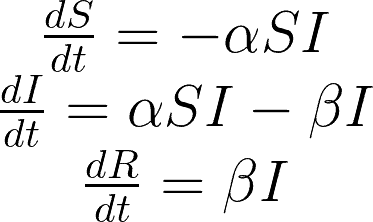
La modifica attuata a questo modello si occupa di inserire un fenomeno fino ad ora mai analizzato, ovvero il “lockdown”, o meglio dire il blocco totale del paese.

È ovvio che il lockdown influenza non di poco l’espansione dell’epidemia, diminuendola in maniera significativa. Questo fenomeno si manifesta all’interno della costante α, ossia la costante diventa una variabile:

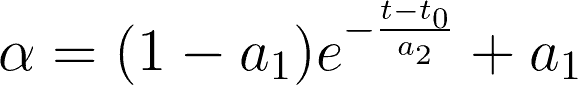
dove a₁, a₂ sono delle costanti da determinare e t₀ è il giorno in cui è stato applicato il lockdown (nel caso dell’Italia il 9 Marzo).

Esiste un metodo matematico, chiamato fitting, che permette di trovare la curva che più si avvicina ai dati reali. In parole povere il fitting modifica i parametri α, β, a₁ e a₂ in modo da seguire il più possibile l’andamento reale dell’epidemia.

Le Figure 5 e 6 mostrano i fit eseguiti sui dati italiani (totale infetti e nuovi infetti al giorno), utilizzando sia il modello S.I.R. modificato sia il modello Richards.

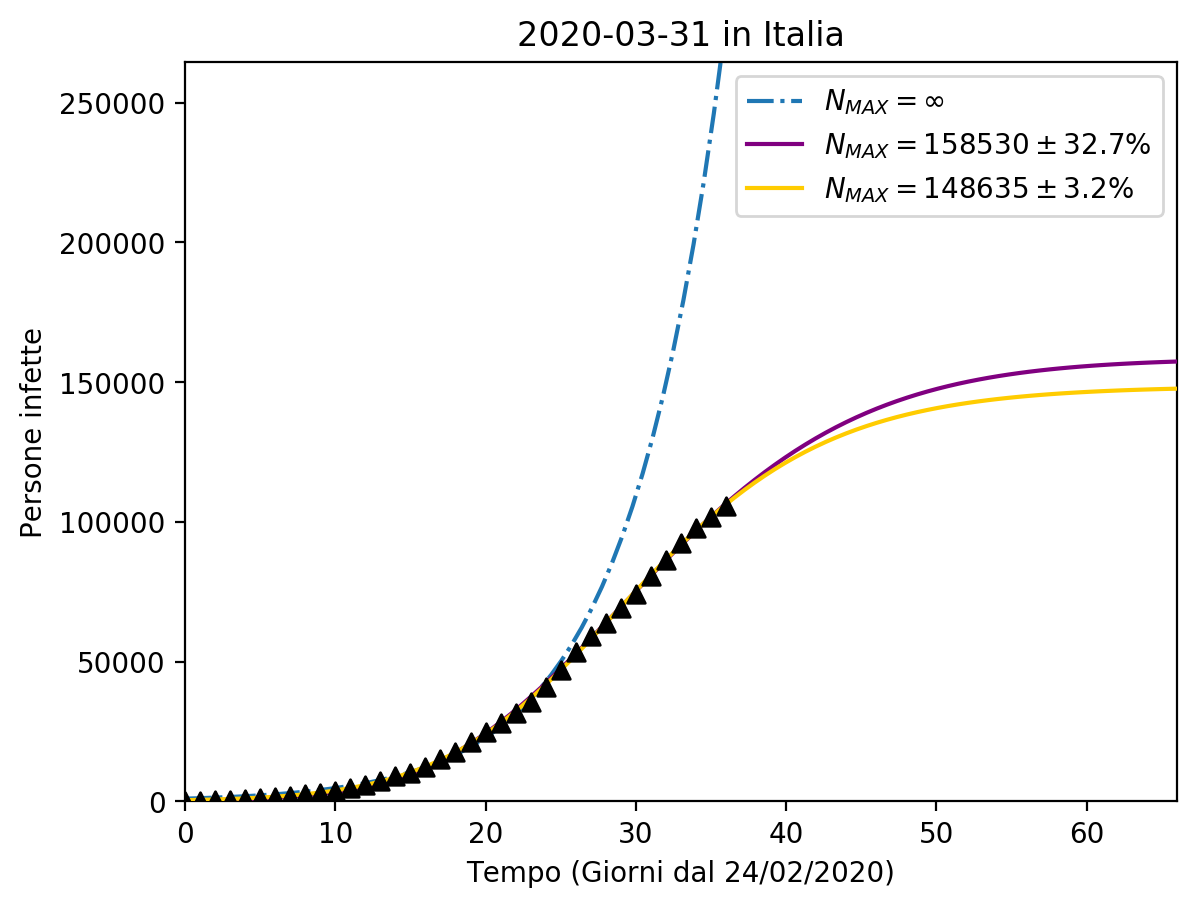
Come si può vedere il modello S.I.R. presenta un errore più grande, perché è più difficile da determinare.

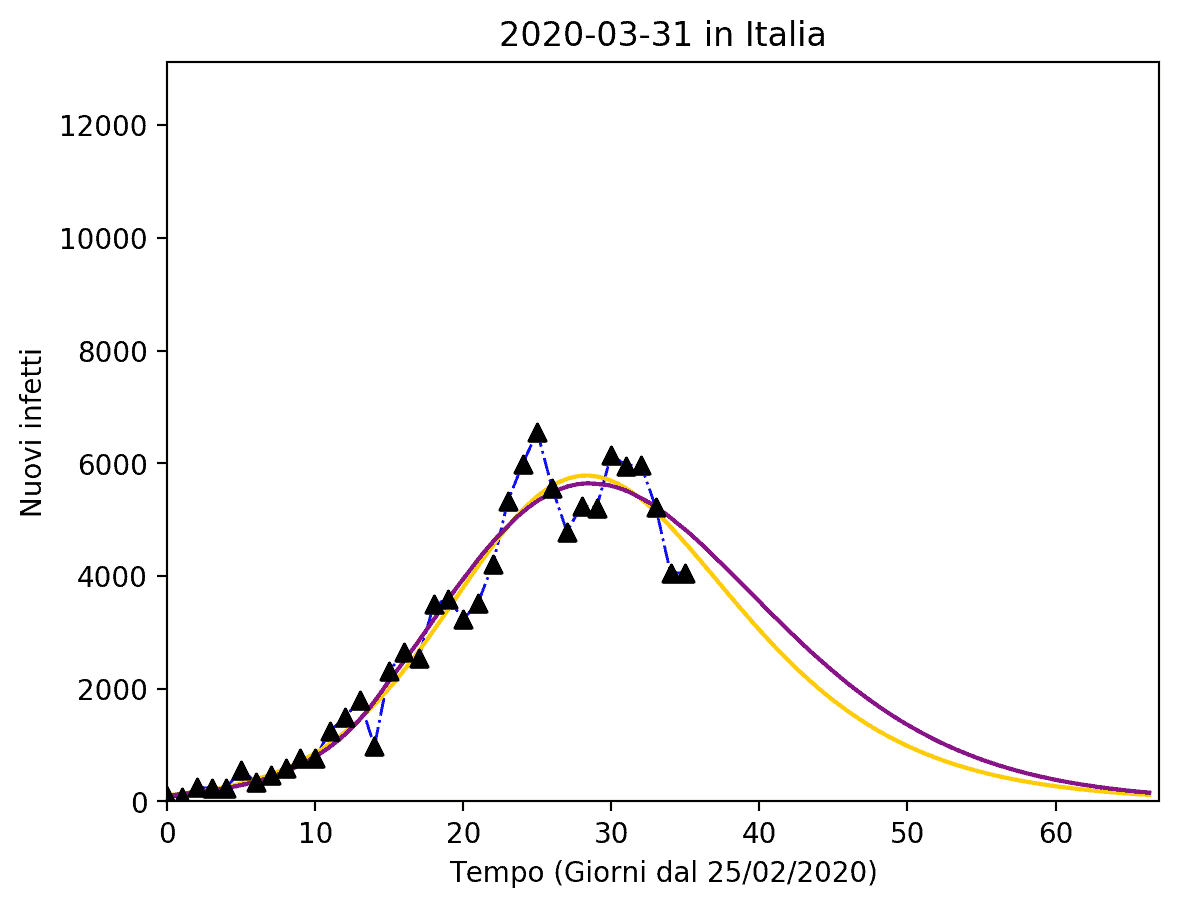
Secondo le teorie quindi l’epidemia dovrebbe essere presente ancora per un altro mese. È ovvio che queste sono solo previsioni matematiche che, come detto nell’introduzione di questo articolo, non prevedono il comportamento inaspettato dell’essere umano.

Quindi, se è vero che sembra di aver superato il picco di contagi, è anche vero che potrebbe continuare a salire se domani ce ne andassimo tutti in giro. Quindi consiglio a tutti quanti di rimanere a casa, perché questa è soltanto la versione più ottimista della situazione attuale.

Potete continuare a seguire l’andamento del virus in tutta Italia e regione per regione al link https://github.com/albertomercurio/covid-19_italy che viene aggiornato giorno dopo giorno.

Alberto Mercurio

[1] https://www.sciencedirect.com/science/article/pii/S0960077920301636